حل دستگاه معادلات خطی به روش حذفی گوس

2015/07/11
نوشته شده توسط متلب24

Gaussian elimination

حل دستگاه معادلات خطی به روش حذفی گوس

روش حذفی گوس روشی در جبر خطی برای حل دستگاه معادلات خطی است. این روش، به صورت انجام عملیات متوالی بر روی ماتریس ضرایب است.

این برنامه به زبان متلب نوشته شده است که n (تعداد معادلات خطی در n معادله n مجهول) را گرفته و سپس ضرایب مجهولات و سپس مقادیر معلوم را دریافت کرده و با استفاده از روش حذفی گوس (Gaussian elimination) معادله را حل و مقادیر مجهولات را بدست آورده و چاپ میکند.

جهت خرید کد متلب روش حذفی گوس از بخش زیر اقدام کنید و بصورت آنلاین خرید و دانلود کنید

[parspalpaiddownloads id=”70″]

ایمیل : matlab24ir@gmail.com و یا info@matlab24.ir

——————————————————

آشنایی با روش حذف گاوسی ( Gaussian elimination) روشی در جبر خطی برای حل دستگاه معادلات خطی است. این روش، به صورت انجام عملیات متوالی بر روی ماتریس ضرایب است. از این روش، همچنین برای یافتن مرتبه‌ی یک ماتریس، محاسبه‌ی دترمینان ماتریس و محاسبه‌ی معکوس یک ماتریس مربعی معکوس‌پذیر استفاده می‌شود. نام این روش از ریاضی‌دان آلمانی کارل فریدریش گاوس گرفته شده است. برای انجام عملیات کاهش سطح در یک ماتریس از یک سری عملیات پایه برروی سطر های ماتریس استفاده می شود. تاماکسیمم مقدار ممکن از درایه های زیر قطر اصلی ماتریس برابر صفر شوند. سه نوع از عملیات پایه برروی سطرهای ماتریس وجود دارد: 1- جابجایی دوردیف از سطرها 2-ضرب کردن یک سطر از ماتریس در یک عدد غیر صفر 3-جمع کردن یک سطر با سطر دیگر. با انجام این عملیات ماتریس به یک ماتریس بالا مثلثی تبدیل می شود(فرم پلکانی). هنگامی که همه ضرایب موثر (سمت چپ ترین داده ها در هر سطر) برابر با یک شوند وبقیه درایه های ستون ها صفر گردند. ماتریس، به یک ماتریس پله ای کاهش یافته تبدیل می شود.و این فرم نهایی، یکتا است. برخی اوقات به روش تبدیل گاوس- جردن می گویند. به دلایل محاسباتی ممکن است، گاهی ترجیح داده شود تا عملیات روی سطر ها قبل از تبدیل متوقف شوند.

پیاده سازی الگوریتم: برای انجام محاسبات می توان این الگوریتم را در کامپیوتر پیاده سازی نمود. شبه کد این الگوریتم به شرح زیر است:

<span class="err">''</span><span class="n">Find</span> <span class="n">the</span> <span class="n">k</span><span class="o">-</span><span class="n">th</span> <span class="nl">pivot</span><span class="p">:</span><span class="err">''</span>
    <span class="nl">i_max</span>  <span class="p">:</span><span class="o">=</span> <span class="p">[[</span><span class="n">argmax</span><span class="p">]]</span> <span class="p">(</span><span class="n">i</span> <span class="o">=</span> <span class="n">k</span> <span class="p">...</span> <span class="n">m</span><span class="p">,</span> <span class="n">abs</span><span class="p">(</span><span class="n">A</span><span class="p">[</span><span class="n">i</span><span class="p">,</span> <span class="n">k</span><span class="p">]))</span>
    <span class="err">'''</span><span class="k">if</span><span class="err">'''</span> <span class="n">A</span><span class="p">[</span><span class="n">i_max</span><span class="p">,</span> <span class="n">k</span><span class="p">]</span> <span class="o">=</span> <span class="mi">0</span>
      <span class="err">'''</span><span class="n">error</span><span class="err">'''</span> <span class="s">"Matrix is singular!"</span>
    <span class="err">'''</span><span class="n">swap</span> <span class="n">rows</span><span class="err">'''</span><span class="p">(</span><span class="n">k</span><span class="p">,</span> <span class="n">i_max</span><span class="p">)</span>
    <span class="err">''</span><span class="n">Do</span> <span class="k">for</span> <span class="n">all</span> <span class="n">rows</span> <span class="n">below</span> <span class="nl">pivot</span><span class="p">:</span><span class="err">''</span>
    <span class="err">'''</span><span class="k">for</span><span class="err">'''</span> <span class="n">i</span> <span class="o">=</span> <span class="n">k</span> <span class="o">+</span> <span class="mi">1</span> <span class="p">...</span> <span class="nl">m</span><span class="p">:</span>
      <span class="err">''</span><span class="n">Do</span> <span class="k">for</span> <span class="n">all</span> <span class="n">remaining</span> <span class="n">elements</span> <span class="n">in</span> <span class="n">current</span> <span class="nl">row</span><span class="p">:</span><span class="err">''</span>
      <span class="err">'''</span><span class="k">for</span><span class="err">'''</span> <span class="n">j</span> <span class="o">=</span> <span class="n">k</span> <span class="o">+</span> <span class="mi">1</span> <span class="p">...</span> <span class="nl">n</span><span class="p">:</span>
        <span class="n">A</span><span class="p">[</span><span class="n">i</span><span class="p">,</span> <span class="n">j</span><span class="p">]</span>  <span class="o">:=</span> <span class="n">A</span><span class="p">[</span><span class="n">i</span><span class="p">,</span> <span class="n">j</span><span class="p">]</span> <span class="o">-</span> <span class="n">A</span><span class="p">[</span><span class="n">k</span><span class="p">,</span> <span class="n">j</span><span class="p">]</span> <span class="o">*</span> <span class="p">(</span><span class="n">A</span><span class="p">[</span><span class="n">i</span><span class="p">,</span> <span class="n">k</span><span class="p">]</span> <span class="o">/</span> <span class="n">A</span><span class="p">[</span><span class="n">k</span><span class="p">,</span> <span class="n">k</span><span class="p">])</span>
      <span class="err">''</span><span class="n">Fill</span> <span class="n">lower</span> <span class="n">triangular</span> <span class="n">matrix</span> <span class="n">with</span> <span class="nl">zeros</span><span class="p">:</span><span class="err">''</span>
      <span class="n">A</span><span class="p">[</span><span class="n">i</span><span class="p">,</span> <span class="n">k</span><span class="p">]</span>  <span class="o">:=</span> <span class="mi">0</span>

''Find the k-th pivot:''

i_max := [[argmax]] (i = k ... m, abs(A[i, k]))

'''if''' A[i_max, k] = 0

'''error''' "Matrix is singular!"

'''swap rows'''(k, i_max)

''Do for all rows below pivot:''

'''for''' i = k + 1 ... m:

''Do for all remaining elements in current row:''

'''for''' j = k + 1 ... n:

A[i, j] := A[i, j] - A[k, j] * (A[i, k] / A[k, k])

''Fill lower triangular matrix with zeros:''

A[i, k] := 0

پیچیدگی محاسباتی

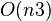پیچیدگی محاسباتی هر الگوریتم با تعداد اجرای هر سطر از آن در کامپیوتر مرتبط است و با نما بیگ O و به فرم $O(n)$ نشان داده می شود. برای مثال برای محاسبه مساله ای با n معادله و n مجهول به روش حذف گاوسی تعداد عمل تقسیم وتعداد عمل ضرب وتعداد عمل تفریق در مجموع به طور تقریبی $2n3/3$ می باشد. بنابراین پیچیدگی ریاضی الگورتیم از مرتبه $O(n3)$ است.