پیاده سازی روش های انتگرال گیری به روش های انتگرال گیری گوسی، انتگرال گیری میانی، قاعده انتگرال گیری سیمپسون، قاعده انتگرال گیری ذوزنقه ای در متلب
پروژه های جبر خطی در متلب
کد متلب انتگرال گیری به روش گوسی
کد متلب انتگرال گیری به روش میانی
کد متلب انتگرال گیری به روش سیمپسون
کد متلب انتگرال گیری به روش ذوزنقه ای
جهت خرید کد متلب روش انتگرال گیری گوسی از لینک زیر اقدام کنید
============================
جهت خرید کد متلب روش انتگرال گیری سیمپسون از لینک زیر اقدام کنید
============================
جهت خرید کد متلب روش انتگرال گیری ذوزنقه ای از لینک زیر اقدام کنید
============================
رمز فایل ها www.matlab24.ir
پشتیبانی: 09120563264
===================================================
توضیحاتی در مورد هر یک از روش ها:
قاعده ذوزنقه‌ای
قاعده ذوزنقه‌ای برای محاسبه مقدار یک انتگرال معین بر پایه تقریب زدن ناحیه بین یک خم و محورx به کمک ذوزنقه‌ها به جای مستطیل‌ها استوار است. طول زیر بازه‌هایی که از تقسیم بازه به کمک نقاط 
بدست می‌آیند، ضرورتی ندارد برابر باشند. اما اگر برابر باشند فرمول حاصل ساده‌تر می‌شود. بنابراین فرض می‌کنیم طول هر زیر بازه چنین باشد:
در قاعده ذوزنقه‌ای قطعات کوچک خم را با پاره‌خطهایی تقریب می‌زنیم. برای برآورد مساحت قسمت‌های مورد سؤال ، مساحتهای ذوزنقه‌هایی را که از وصل کردن دو سر این پاره‌خطها به محور x ایجاد می‌شوند جمع می‌کنیم. بنابراین برای تقریب زدن 
توسط قاعده ذوزنقه‌ای از رابطه زیر استفاده می‌کنیم: (طول هر یک از 
است)
ضمنا داریم: 
برآورد خطا در قاعده ذوزنقه‌ای
اگر f پیوسته و M یک کران بالا برای مقادیر 
روی 
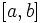باشد آنگاه خطای 
در تقریب ذوزنقه‌ای انتگرال f از a تا b در نابرابری زیر صدق می‌کند.
- قاعده ذوزنقه‌ای برای چند جمله‌ایها تا درجه دوم دقیق تر است.
قاعده سیمپسون
هر سه نقطه‌ای از یک صفحه را که روی یک خط راست واقع نباشند می‌توان روی یک سهمی جای داد. قاعده سیمپسون بر پایه تقریب‌زدن خم‌ها با سهمی D به عوض ذوزنقه‌ها استوار است مساحت قسمت دلخواه از زیر سهمی با بکاربردن پیاپی فرمول زیر در سراسر خم پیوسته 
از x=a تا x=b برآوردی از 
بدست می‌دهد که معمولا برای یک اندازه گام مفروض h ، از T دقیق‌تر است:
بنابراین برای تقریب‌زدن توسط قاعده سیمپسون فرمول زیر را بکار می‌بریم:
توجه: n زوج است و می‌باشد.
همان‌طور که مشهود است قاعده ذوزنقه‌ای بسیار کند است، به عبارت دیگر برای بدست‌آوردن تقریبی نه چندان دقیقی باید تابع را در نقاط بسیاری محاسبه کرد. روش سیمپسون برای محاسبات دستی بسیار ساده و نسبتا دقیق است. برای مثال تقریبی از 
به قاعده سیمپسون با 
بصورت زیر است:
::
، 
نسبتا دقیق است.
برآورد خطا در قاعده سیمپسون
اگر 
پیوسته و M یک کران بالا برای مقادیر 
روی 
باشد آنگاه خطای 
در تقریب سیمپسون انتگرال f از a تا b در نابرابری زیر صدق می‌کند:
- قاعده سیمپسون برای چندجمله‌ایها تا درجه سوم دقیق‌تر است.
