الگوریتم دسته ماهی های مصنوعی
Artificial Fish Swarm Algorithm
الگوریتم ماهی های مصنوعی
- الگوریتم دسته ماهی های مصنوعی (AFSA) جزء الگوریتم های هوش جمعی می باشد و کاربرد عمده آن در حل مسائل بهینه سازی است.
- AFSA گونه ای از الگوریتم های برگرفته شده از طبیعت می باشد که توسط دکتر Li Xiao Lei در سال ٢٠٠٢ ارائه شده است.
- این الگوریتم تکنیکی مبتنی بر رفتارهای جمعی است که از رفتار های اجتماعی دسته ماهی ها در طبیعت الهام گرفته شده است.
جهت دریافت کد متلب الگوریتم ماهی های مصنوعی با ما تماس بگیرید
شماره تماس : 09120563264
ایمیل :matlab24ir@gmail.com و یا info@matlab24.ir
—————————————————————————————————————————————
- مدل ماهی مصنوعی شامل دو بخش متغیرها و توابع است:
1 – متغیرها:
- X : موقعیت فعلی ماهی مصنوعی
- Step : حداکثر طول گام حرکت
- Visual : میدان دید هر ماهی
- try_number : سقف تعداد آزمایش و سعی کردن
- δ : فاکتور شلوغی هر منطقه از فضای جستجو که 0<δ<1
٢ – توابع:
کلیات الگوریتم :
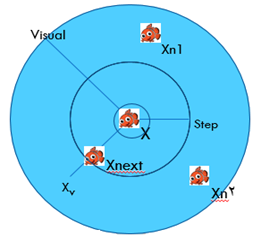
- وضعیت فعلی ماهی مصنوعی توسط بردار X = (x1,x2,…,xn) نشان داده میشود.
- Visual برابر میدان دید ماهی مصنوعی میباشد.
- Step برابر حداکثر طول گام حرکت است.
-
الگوریتم دسته ماهی های مصنوعی
- Xv موقعیتی در میدان دید است که ماهی مصنوعی میخواهد به آنجا برود. حال اگر وضعیت Xv از نظر تراکم غذایی بهتر از وضعیت فعلی باشد ، یک گام به جلو در جهت آن پیش میرویم که باعث تغییر وضعیت ماهی مصنوعی از X به Xnext میشود. ولی اگر وضعیت فعلی بهتر از Xv باشد ، به گشت زنی در محدوده میدان دید ادامه میدهیم.
- فاصله بین دو ماهی مصنوعی که در وضعیت های Xi و Xj هستند با رابطه dij = ǁXi – Xjǁ نشان داده میشود ( فاصله اقلیدسی ).
رفتار حرکت آزادانه :
در طبیعت هنگامی که ماهی ها موفق به یافتن غذا نشوند ، به صورت آزادانه حرکت میکنند.
در AFSA هنگامی که ماهی مصنوعی نتواند به سمت موقعیتی با مقدار غذای بیشتر حرکت کند ، یک گام به صورت تصادفی با فرمول زیر در فضای مسئله حرکت میکند:
Xi(t+1)=Xi(t)+Step.Rand(-1,1)
که در آن ، Xi برابر بردار موقعیت ماهی مصنوعی iام در فضای D بعدی است.
تابع Rand یک بردار D بعدی از اعداد تصادفی جداگانه را در بازه [-1,1] با توزیع یکنواخت تولید میکند.
