آموزش خوشه بندی سلسه مراتبی
خوشهبندي سلسله مراتبي (Hierarchical) و خوشهبندي مسطح(Flat)
در روش خوشه بندي سلسله مراتبي، به خوشههاي نهايي بر اساس ميزان عموميت آنها ساختاري سلسله مراتبي نسبت داده ميشود. مانند روشSingle Link. ولي در خوشهبندي مسطح تمامي خوشههاي نهايي داراي يک ميزان عموميت هستند مانندK-Means. به ساختار سلسله مراتبي حاصل از روشهاي خوشهبندي سلسله مراتبي دندوگرام (Dendogram) گفته ميشود.
با توجه با اينکه روشهاي خوشهبندي سلسله مراتبي اطلاعات بيشتر و دقيقتري توليد ميکنند براي تحليل دادههاي با جزئيات پيشنهاد ميشوند ولي از طرفي چون پيچيدگي محاسباتي بالايي دارند براي مجموعه دادههاي بزرگ روشهاي خوشهبندي مسطح پيشنهاد ميشوند.
روشهاي خوشهبندي سلسله مراتبي
همان گونه که بيان شد، در روش خوشه بندي سلسله مراتبي، به خوشههاي نهايي بر اساس ميزان عموميت آنها ساختاري سلسله مراتبي، معمولا به صورت درختي نسبت داده ميشود. به ا ين درخت سلسله مراتبي دندوگرام (dendogram) ميگويند. روش کار تکنيکهاي خوشهبندي سلسلهمراتبي معمولا بر اساس الگوريتمهاي حريصانه (Greedy Algorithms) و بهينگي مرحلهاي (stepwise-optimal) است. روشهاي خوشهبندي بر اساس ساختار سلسله مراتبي توليدي توسط آنها معمولا به دو دستة زير تقسيم ميشوند:
- بالا به پايين (Top-Down) يا تقسيم کننده (Divisive): در اين روش ابتدا تمام دادهها به عنوان يک خوشه در نظر گرفته ميشوند و سپس در طي يک فرايند تکراري در هر مرحله دادههايي شباهت کمتري به هم دارند به خوشههاي مجزايي شکسته ميشوند و اين روال تا رسيدن به خوشههايي که داراي يک عضو هستند ادامه پيدا ميکند.
- پايين به بالا (Bottom-Up) يا متراکم شونده (Agglomerative): در اين روش ابتدا هر دادهها به عنوان خوشهاي مجزا در نظر گرفته ميشود و در طي فرايندي تکراري در هر مرحله خوشههايي که شباهت بيشتري با يکديگر با يکديگر ترکيب ميشوند تا در نهايت يک خوشه و يا تعداد مشخصي خوشه حاصل شود. از انواع الگوريتمهاي خوشهبندي سلسله مراتبي متراکم شونده رايج ميتوان از الگوريتمهايSingle-Link، Average-Link و Complete-Link نام برد. تفاوت اصلي در بين تمام اين روشها به نحوة محاسبة شباهت بين خوشهها مربوط ميشود. که در بخشهاي بعد به تشريح هر يک پرداخته خواهد شد.
نمونهاي از روش خوشهبندي سلسله مراتبي و تفاوت بين روشهاي بالا به پايين و پايين به بالا در شکل زير مشاهده ميشود.
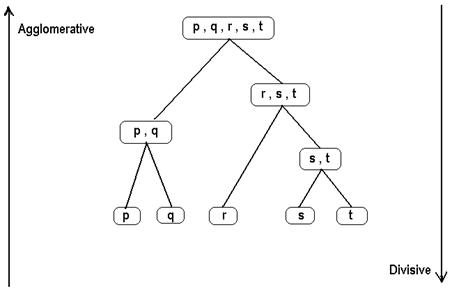
شکل 3: تفاوت بين روشهاي بالا به پايين با روشهاي پايين به بالا
ا
خوشهبندي با روش Single-Link
اين روش يکي از قديميترين و سادهترين روشهاي خوشهبندي است و جزء روشهاي خوشهبندي سلسله مراتبي و انحصاري محسوب ميشود. به اين روش خوشهبندي، تکنيک نزديکترين همسايه (Nearest Neighbour) نيز گفته ميشود. در اين روش براي محاسبة شباهت بين دو خوشة A و B از معيار زير استفاده ميشود:
که i يک نمونه داده متعلق به خوشة A و j يک نمونه دادة متعلق به خوشة B ميباشد. در واقع در اين روش شباهت بين دو خوشه، کمترين فاصلة بين يک عضو از يکي با يک عضو از ديگري است. در شکل زير اين مفهوم بهتر نشان داده شده است. [5]
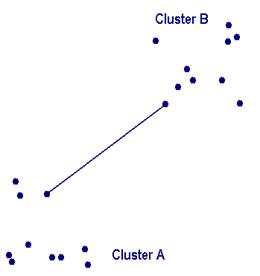
شکل 4: شباهت بين دو خوشه در روش Single-Link برابر است با کمترين فاصلة بين دادههاي دو خوشه
1-1-1- مثال: در اين قسمت سعي شده است تا در مثالي با فرض داشتن 6 نمونه داده و ماتريس فاصلة بين آنها که در جدول 1 نشانداده شده است، نحوة اعمال روش خوشهبندي Single-Link بهتر تشريح شود.
جدول 1: ماتريس فاصلة بين 6 نمونة داده
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | 0 | 4 | 13 | 24 | 12 | 8 |
| 2 | 0 | 10 | 22 | 11 | 10 | |
| 3 | 0 | 7 | 3 | 9 | ||
| 4 | 0 | 6 | 18 | |||
| 5 | 0 | 8.5 | ||||
| 6 | 0 |
در ابتدا هر داده به عنوان يک خوشه در نظر گرفته ميشود و يافتن نزديکترين خوشه در واقع يافتن کمترين فاصلة بين دادههاي بالا خواهد بود. با توجه به جدول 1 مشخص است که دادههاي 3 و 5 کمترين فاصله را دارا هستند. و در نتيجه آنها را با هم ترکيب کرده و خوشة جديدي حاصل ميشود که فاصلة آن از ساير خوشهها برابر است با کمترين فاصلة بين 3 و يا 5 از ساير خوشهها. نتيجه در جدول 2 نشان داده شده است.
جدول 2: ماتريس فاصلة بين 5 خوشة حاصل از تکرار اول
| 1 | 2 | (3 و 5) | 4 | 6 | |
| 1 | 0 | 4 | 12 | 24 | 8 |
| 2 | 0 | 10 | 22 | 10 | |
| (3 و 5) | 0 | 6 | 8.5 | ||
| 4 | 0 | 18 | |||
| 6 | 0 |
با توجه به جدول 2 مشخص است که دادههاي 1 و 2 کمترين فاصله را دارا هستند. و در نتيجه آنها را با هم ترکيب کرده و خوشة جديدي حاصل ميشود که فاصلة آن از ساير خوشهها برابر است با کمترين فاصلة بين 1 و يا 2 از ساير خوشهها. نتيجه در جدول 3 نشان داده شده است.
جدول 3: ماتريس فاصلة بين 4 خوشة حاصل از تکرار دوم
| (1 و 2) | (3 و 5) | 4 | 6 | |
| (1 و 2) | 0 | 10 | 22 | 8 |
| (3 و 5) | 0 | 6 | 8.5 | |
| 4 | 0 | 18 | ||
| 6 | 0 |
با توجه به جدول 3 مشخص است که خوشههاي (3 و 5) و 4 کمترين فاصله را دارا هستند. و در نتيجه آنها را با هم ترکيب کرده و خوشة جديدي حاصل ميشود که فاصلة آن از ساير خوشهها برابر است با کمترين فاصلة بين (3 و 5) و يا 4 از ساير خوشهها. نتيجه در جدول4 نشان داده شده است.
جدول 4: ماتريس فاصلة بين 3 خوشة حاصل از تکرار سوم
| (1 و 2) | (3، 4 و 5) | 6 | |
| (1 و 2) | 0 | 10 | 8 |
| (3، 4 و 5) | 0 | 8.5 | |
| 6 | 0 |
با توجه به جدول 4 مشخص است که خوشههاي (1 و 2) و 6 کمترين فاصله را دارا هستند. و در نتيجه آنها را با هم ترکيب کرده و خوشة جديدي حاصل ميشود که فاصلة آن از ساير خوشهها برابر است با کمترين فاصلة بين (1 و 2) و يا 6 از ساير خوشهها. نتيجه در جدول5 نشان داده شده است.
جدول 5: ماتريس فاصلة بين 2 خوشة حاصل از تکرار چهارم
| (1، 2 و 6) | (3، 4 و 5) | |
| (1، 2 و 6) | 0 | 8.5 |
| (3، 4 و 5) | 0 |
در نهايت اين دو خوشة حاصل ا هم ترکيب ميشوند. نتيجه در دندوگرام شکل 5 نشان داده شده است.
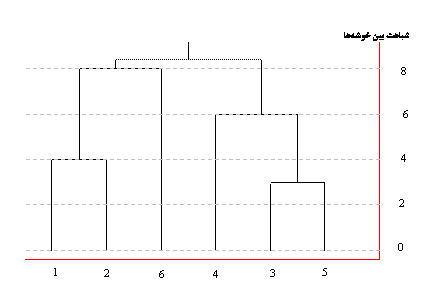
شکل 5: دندوگرام مثال Single-Link
خوشهبندي با روش Complete-Link
این روش همانند Single-Link جزء روشهاي خوشهبندي سلسله مراتبي و انحصاري محسوب ميشود. به اين روش خوشهبندي، تکنيک دورترين همسايه (furthest Neighbour) نيز گفته ميشود. در اين روش براي محاسبة شباهت بين دو خوشة Aو B از معيار زير استفاده ميشود:
(2)
که i يک نمونه داده متعلق به خوشة A و j يک نمونه دادة متعلق به خوشة B ميباشد. در واقع در اين روش شباهت بين دو خوشه بيشترين فاصلة بين يک عضو از يکي با يک عضو از ديگري است. در شکل زير اين مفهوم بهتر نشان داده شده است. [5]
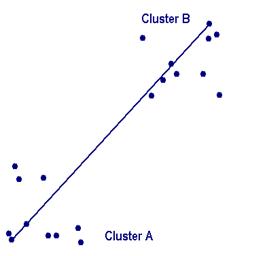
شکل 6: شباهت بين دو خوشه در روش Complete-Link برابر است با بيشترين فاصلة بين دادههاي دو خوشه.
مثال: در اين قسمت سعي شده است تا در مثالي با فرض داشتن 6 نمونه داده و ماتريس فاصلة بين آنها که در جدول 6 نشان داده شده است، نحوة اعمال روش خوشهبنديComplete-Link بهتر تشريح شود.
جدول 6: ماتريس فاصلة بين 6 نمونة داده
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | 0 | 4 | 13 | 24 | 12 | 8 |
| 2 | 0 | 10 | 22 | 11 | 10 | |
| 3 | 0 | 7 | 3 | 9 | ||
| 4 | 0 | 6 | 18 | |||
| 5 | 0 | 8.5 | ||||
| 6 | 0 |
در ابتدا هر داده به عنوان يک خوشه در نظر گرفته ميشود و يافتن نزديکترين خوشه در واقع يافتن کمترين فاصلة بين دادههاي بالا خواهد بود. با توجه به جدول 6 مشخص است که دادههاي 3 و 5 کمترين فاصله را دارا هستند. و در نتيجه آنها را با هم ترکيب کرده و خوشة جديدي حاصل ميشود که فاصلة آن از ساير خوشهها برابر است بابيشترين فاصلة بين 3 و يا 5 از ساير خوشهها. نتيجه در جدول 7 نشان داده شده است.
جدول 7: ماتريس فاصلة بين 5 خوشة حاصل از تکرار اول
| 1 | 2 | (3 و 5) | 4 | 6 | |
| 1 | 0 | 4 | 13 | 24 | 8 |
| 2 | 0 | 11 | 22 | 10 | |
| (3 و 5) | 0 | 7 | 9 | ||
| 4 | 0 | 18 | |||
| 6 | 0 |
با توجه به جدول 7 مشخص است که دادههاي 1 و 2 کمترين فاصله را دارا هستند. و در نتيجه آنها را با هم ترکيب کرده و خوشة جديدي حاصل ميشود که فاصلة آن از ساير خوشهها برابر است با بيشترين فاصلة بين 1 و يا 2 از ساير خوشهها. نتيجه در جدول 8 نشان داده شده است.
جدول 8: ماتريس فاصلة بين 4 خوشة حاصل از تکرار دوم
| (1 و 2) | (3 و 5) | 4 | 6 | |
| (1 و 2) | 0 | 13 | 24 | 10 |
| (3 و 5) | 0 | 7 | 9 | |
| 4 | 0 | 18 | ||
| 6 | 0 |
با توجه به جدول 8 مشخص است که خوشههاي (3 و 5) و 4 کمترين فاصله را دارا هستند. و در نتيجه آنها را با هم ترکيب کرده و خوشة جديدي حاصل ميشود که فاصلة آن از ساير خوشهها برابر است با بيشترين فاصلة بين (3 و 5) و يا 4 از ساير خوشهها. نتيجه در جدول 9 نشان داده شده است.
جدول 9: ماتريس فاصلة بين 3 خوشة حاصل از تکرار سوم
| (1 و 2) | (3، 4 و 5) | 6 | |
| (1 و 2) | 0 | 24 | 10 |
| (3، 4 و 5) | 0 | 18 | |
| 6 | 0 |
با توجه به جدول 9 مشخص است که خوشههاي (1 و 2) و 6 کمترين فاصله را دارا هستند. و در نتيجه آنها را با هم ترکيب کرده و خوشة جديدي حاصل ميشود که فاصلة آن از ساير خوشهها برابر است با بيشترين فاصلة بين (1 و 2) و يا 6 از ساير خوشهها. نتيجه در جدول 10 نشان داده شده است.
جدول 10: ماتريس فاصلة بين 2 خوشة حاصل از تکرار چهارم
| (1، 2 و 6) | (3، 4 و 5) | |
| (1، 2 و 6) | 0 | 24 |
| (3، 4 و 5) | 0 |
در نهايت اين دو خوشة حاصل ا هم ترکيب ميشوند. نتيجه در دندوگرام شکل 7 نشان داده شده است.

شکل 7: دندوگرام مثال Complete-Link
خوشهبندي با روش Average-Link
اين روش همانند Single-Link جزء روشهاي خوشهبندي سلسله مراتبي و انحصاري محسوب ميشود. از آنجا که هر دو روش خوشهبندي Single-link و Complete-link بشدت به نويز حساس ميباشد، اين روش که محاسبات بيشتري دارد، پيشنهاد شد. در اين روش براي محاسبة شباهت بين دو خوشة A و B از معيار زير استفاده ميشود:
(3)
که i يک نمونه داده متعلق به خوشة A و j يک نمونه دادة متعلق به خوشة B ميباشد. و NA تعداد اعضاء خوشة A و NB تعداد اعضاء خوشة B است. در واقع در اين روش، شباهت بين دو خوشه ميانگين فاصلة بين تمام اعضاء يکي با تمام اعضاء ديگري است. در شکل زير اين مفهوم بهتر نشان داده شده است. [5]
شکل 8: شباهت بين دو خوشه در روش Average-Link برابر است با ميانگين فاصلة بين دادههاي دو خوشه
مثال: در اين قسمت سعي شده است تا در مثالي با فرض داشتن 6 نمونه داده و ماتريس فاصلة بين آنها که در جدول 11 نشان داده شده است، نحوة اعمال روش خوشهبنديAverage-Link بهتر تشريح شود.
جدول 11: ماتريس فاصلة بين 6 نمونة داده
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 1 | 0 | 4 | 13 | 24 | 12 | 8 |
| 2 | 0 | 10 | 22 | 11 | 10 | |
| 3 | 0 | 7 | 3 | 9 | ||
| 4 | 0 | 6 | 18 | |||
| 5 | 0 | 8.5 | ||||
| 6 | 0 |
در ابتدا هر داده به عنوان يک خوشه در نظر گرفته ميشود و يافتن نزديکترين خوشه در واقع يافتن کمترين فاصلة بين دادههاي بالا خواهد بود. با توجه به جدول 11 مشخص است که دادههاي 3 و 5 کمترين فاصله را دارا هستند. و در نتيجه آنها را با هم ترکيب کرده و خوشة جديدي حاصل ميشود که فاصلة آن از ساير خوشهها برابر است باميانگين فاصلة بين 3 و 5 از ساير خوشهها. نتيجه در جدول 12 نشان داده شده است.
جدول 12: ماتريس فاصلة بين 5 خوشة حاصل از تکرار اول
| 1 | 2 | (3 و 5) | 4 | 6 | |
| 1 | 0 | 4 | 12.5 | 24 | 8 |
| 2 | 0 | 10.5 | 22 | 10 | |
| (3 و 5) | 0 | 6.5 | 8.75 | ||
| 4 | 0 | 18 | |||
| 6 | 0 |
با توجه به جدول 12 مشخص است که دادههاي 1 و 2 کمترين فاصله را دارا هستند. و در نتيجه آنها را با هم ترکيب کرده و خوشة جديدي حاصل ميشود که فاصلة آن از ساير خوشهها برابر است با بيشترين فاصلة بين 1 و يا 2 از ساير خوشهها. نتيجه در جدول 13 نشان داده شده است.
جدول 13: ماتريس فاصلة بين 4 خوشة حاصل از تکرار دوم
| (1 و 2) | (3 و 5) | 4 | 6 | |
| (1 و 2) | 0 | 11.5 | 23 | 9 |
| (3 و 5) | 0 | 6.5 | 8.75 | |
| 4 | 0 | 18 | ||
| 6 | 0 |
با توجه به جدول 13 مشخص است که خوشههاي (3 و 5) و 4 کمترين فاصله را دارا هستند. و در نتيجه آنها را با هم ترکيب کرده و خوشة جديدي حاصل ميشود که فاصلة آن از ساير خوشهها برابر است با بيشترين فاصلة بين (3 و 5) و يا 4 از ساير خوشهها. نتيجه در جدول 14 نشان داده شده است.
جدول 14: ماتريس فاصلة بين 3 خوشة حاصل از تکرار سوم
| (1 و 2) | (3، 4 و 5) | 6 | |
| (1 و 2) | 0 | 23 | 9 |
| (3، 4 و 5) | 0 | 18 | |
| 6 | 0 |
با توجه به جدول 14 مشخص است که خوشههاي (1 و 2) و 6 کمترين فاصله را دارا هستند. و در نتيجه آنها را با هم ترکيب کرده و خوشة جديدي حاصل ميشود که فاصلة آن از ساير خوشهها برابر است با بيشترين فاصلة بين (1 و 2) و يا 6 از ساير خوشهها. نتيجه در جدول 15 نشان داده شده است.
جدول 15: ماتريس فاصلة بين 2 خوشة حاصل از تکرار چهارم
| (1، 2 و 6) | (3، 4 و 5) | |
| (1، 2 و 6) | 0 | 20.5 |
| (3، 4 و 5) | 0 |
در نهايت اين دو خوشة حاصل ا هم ترکيب ميشوند. نتيجه در دندوگرام شکل 9 نشان داده شده است.

شکل 9: دندوگرام مثال Average-Lin