آموزش الگوريتم خوشه بندی C ميانگين (Fuzzy C-Means)
یکی از مهمترین و پرکاربردترین الگوریتم های خوشه بندی، الگوریتم c میانگین می باشد. در این الگوریتم نمونه ها به c خوشه تقسیم می شوند و تعداد c از قبل مشخص شده است. در نسخه فازی این الگوریتم نیز تعداد خوشه ها (c) از قبل مشخص شده است. در الگوریتم خوشه بندی c میانگین فازی تابع هدف بصورت زیر می باشد:
جهت خواندن ادامه ،به بخش ادامه مطلب مراجعه نمایید
جهت دریافت کد متلب الگوريتم Fuzzy C-Means اینجا را ببینید
ایمیل : matlab24ir@gmail.com و یا info@matlab24.ir
شماره تماس : 09120563264
آموزش الگوريتم خوشه بندی C ميانگين (Fuzzy C-Means)
یکی از مهمترین و پرکاربردترین الگوریتم های خوشه بندی، الگوریتم c میانگین می باشد. در این الگوریتم نمونه ها به c خوشه تقسیم می شوند و تعداد c از قبل مشخص شده است. در نسخه فازی این الگوریتم نیز تعداد خوشه ها (c) از قبل مشخص شده است. در الگوریتم خوشه بندی c میانگین فازی تابع هدف بصورت زیر می باشد:
در فرمول فوق m یک عدد حقیقی بزرگتر از 1 است که در اکثر موراد برای m عدد 2 انتخاب می شود. اگر در فرمول فوق m را برابر 1 قرار دهیم تابع هدف خوشه بندی c میانگین (کلاسیک) غیر فازی بدست می آید. در فرمول فوق xk نمونه k ام و vi نماینده یا مرکز خوشه i ام و n تعداد نمونه ها می باشد.uikمیزان تعلق نمونه i ام در خوشه k ام را نشان می دهد. علامت ||*|| میزان تشابه (فاصله) نمونه با (از) مرکز خوشه می باشد که می توان از هر تابعی که بیانگر تشابه نمونه و مرکز خوشه باشد استفاده کرد. از روی uikمی توان یک ماتریس U تعریف کرد که دارای c سطر و n ستون می باشد و مولفه های آن هر مقداری بین 0 تا 1 را می توانند اختیار کنند. اگر تمامی مولفه های ماتریس U بصورت 0 و یا 1 باشند الگوریتم مشابه c میانگین کلاسیک خواهد بود. با اینکه مولفه های ماتریس U می توانند هر مقداری بین 0 تا 1 را اختیار کنند اما مجموع مولفه های هر یک از ستونها باید برابر 1 باشد و داریم:
معنای این شرط این است که مجموع تعلق هر نمونه به c خوشه باید برابر 1 باشد. برای بدست آوردن فرمولهای مربوط به uik و vi باید تابع هدف تعریف شده را می نیمم کنیم. با استفاده از شرط فوق و برابر صفر قرار دادن مشتق تابع هدف خواهیم داشت:
و
با استفاده از دو فرمول محاسبه شده الگویتم خوشه بندی c میانگین فازی بصورت زیر می باشد.
مراحل الگوریتم:
1.مقدار دهی اولیه برای c، m و U0. خوشه های اولیه حدس زده شوند.
2.مراکز خوشه ها محاسبه شوند (محاسبه viها).
3.محاسبه ماتریس تعلق از روی خوشه های محاسبه شده در 2.
4.اگر ||Ul+1–Ul|| £ e الگوریتم خاتمه می یابد و در غیر اینصورت برو به مرحله 2.
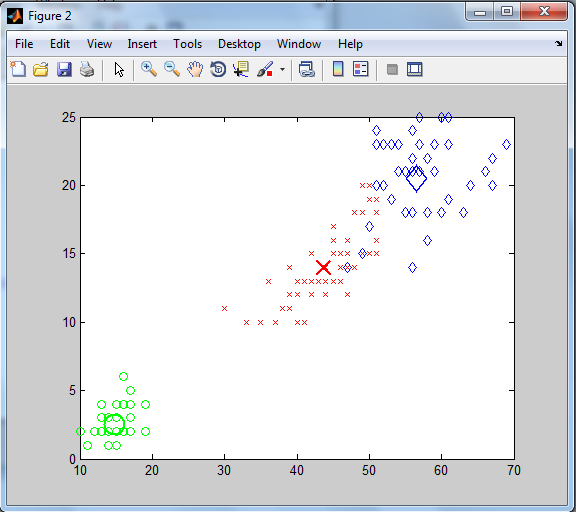
برای مشاهده عملکرد خوشه بندی فازی به مثال زیر توجه کنید. در شکل زیر یک توزیع یک بعدی از نمونه های ورودی را آورده شده است.
اگر از الگوریتم c میانگین کلاسیک استفاده کنیم داده های فوق به دو خوشه مجزا تقسیم خواهند شد و هر نمونه تنها متعلق به یکی از خوشه ها خواهد بود. بعبارت دیگر تابع تعلق هر نمونه مقدار 0 یا 1 خواهد داشت. نتیجه خوشه بندی کلاسیک مطابق شکل زیر است:
شکل 2 تابع تعلق مربط به خوشه A را نشان می دهد. تابع تعلق خوشه B متمم تابع تعلق A می باشد. همانطور که مشاهده می کنید نمونه های ورودی تنها به یکی از خوشه ها تعلق دارند و بعبارت دیگر ماتریس U بصورت باینری می باشد. حال اگر از خوشه بندی فازی استفاده کنیم خواهیم داشت:
مشاهده می کنید که در این حالت منحنی تابع تعلق هموارتر است و مرز بین خوشه ها بطور قطع و یقین مشخص نشده است. بعنوان مثال نمونه ای که با رنگ قرمز مشخص شده است با درجه تعلق 0.2 به خوشه A و با درجه تعلق 0.8 به خوشه B نسبت داده شده است.
نقاط قوت الگوریتم c میانگین فازی:
همیشه همگرا می شود.
بدون نظارت بودن الگوریتم.
نقاط ضعف الگوریتم c میانگین فازی:
زمان محاسبات زیاد است.
حساس به حدسهای اولیه میباشد و ممکن در مینیمم های محلی متوقف شود.
حساس به نویز می باشد.
اگر معیار تشابه در تابع هدف بر اساس فاصله تعریف شود می توان از تعاریف مختلفی که در مورد فاصله وجود دارد استفاده کرد که در زیر چند نمونه از این توابع آورده شده است: