یکی از مسائل معروف در حوزه بهینه سازی ، مسئله کوله پشتی یا Knapsack Problem می باشد.
هدف از مسئله کوله پشتی، یافتن ماکزیمم ارزش از اجسامی است که در یک کوله پشتی با ظرفیت محدود میتوان قرار داد.
چطور بصورت بهینه، از بین لوازم موجود، با ارزشترین ها را در کوله پشتی قرار دهیم؟

سرفصل های آموزش جامع و کامل مسئله کوله پشتی
آشنایی با مسئله کوله پشتی : مثال دزد باهوش!
یه روز یه دزد باهوش وارد یک خانه ای پر از لوازم قیمتی و با ارزش میشود ، که همه لوازمش لوکس و قیمتی بودن.
از مبل های لوکس و گران قیمت تا لوازم عتیقه و تابلو فرش های کمیاب و طلا و جواهراتی که در خانه بود تا اسکناس های نقدی که در گاوصندوق قرار داشت.
فقط این دزد خوش شانس تنها مشکلی که داشت این بود که دیسک کمر داشت و نمیتونست بیشتر از 20 کیلوگرم رو بلند کنه و با خودش ببره .
البته همونطور که گفتم دزد مورد صحبت باهوش بود و برای اینکه در حین دزدی ، وسوسه نشه
و بیشتر از 20 کیلو رو برنداره ، برای خود یک کیسه ساخته بود که فقط 20 کیلوگرم ظرفیت داشت
و در نتیجه با خیال راحت لوازمی که میخواست رو برمیداشت و داخل کیسه اش می گذاشت
و وقتی که کیسه اش پر میشد ، دیگه دست از دزدی بر میداشت و پا به فرار میگذاشت.
خب حالا دزد باهوش، که امروز روی شانس هم بوده و وارد خانه ای پر از لوازم با ارزش شده ،
فکرش حسابی درگیره که چی چیزایی رو برداره که هم بیشتر از ظرفیت کیسه اش یعنی 20 کیلو وزن نداشته باشند
و هم اینکه بعدا که بخواد اون وسایل رو بفروشه، به بیشترین مقدار بتونه بفروشه و بیشترین سود ممکن رو از این دزدی برده باشه.
بهترین کار ، هنگام حل یک چالش و مسئله ، این هست که ابتدا ساده سازی کنیم و بعد فرموله بندی کنیم. تا بتوانیم مسئله را به بهترین شکل حل کنیم.
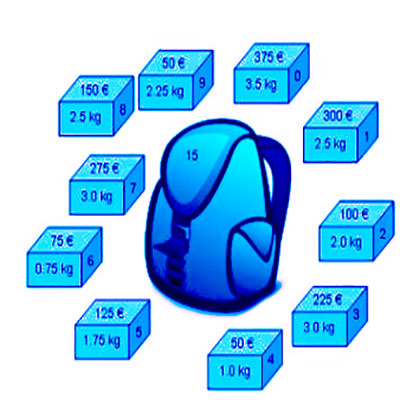
مجموعه ای از وسایل داریم که آنها را با اعداد 1 تا n شماره گذازی میکنیم.
هر کدوم از وسایل وزن خاص خود را دارد که وزن آنها را نیز با علامت های w1 تا wn نشان میدهیم.
هر کدام از وسایل ، ارزش خاص خود را دارد که ارزش اشیا را با v1 تا vn نشان میدهیم.
پس شی شماره 1 دارای وزن w1 و ارزش v1 می باشد،
شی شماره 2 دارای وزن w2 و ارزش v2 می باشد،
شی شماره 3 دارای وزن w3 و ارزش v3 می باشد.
بهتره باز هم ساده تر کنیم : 2 تا آرایه در نظر میگیریم.
آرایه شماره 1: وزن وسایل را نگهداری میکند.
آرایه شماره 2 : ارزش وسایل را در آن قرار میدهیم.

خب حالا که مسئله را ساده سازی کردیم ، تکلیف آقا دزده چی میشه؟ کدوم وسایل رو برداره که هم مجموع وزنشون بیشتر از 20 کیلوگرم نشه ، هم ارزششون ماکزیمم ترین حالت ممکن باشه؟!
چرا مسئله کوله پشتی مهم است؟
قطعا هدف ما در اینجا از ارائه راه حل ، کمک کردن به آقای دزد مثالمان نیست و در واقع مسئله کوله پشتی ، دارای مسائل مشابه در دنیای واقعی است که حل بهینه آنها میتواند کمک زیادی به کاهش هزینه و افزایش بهره وری در کارهای مختلف ، مانند مسائل تخصیص منابع ، رمزنگاری و سایر مسائل مشابه بکند.
تحقیقات زیادی برای یافتن پاسخ بهینه مسئله کوله پشتی در سالهای مختلف انجام شده است ، ابتدا روش های برگشت به عقب مطرح شد ، سپس حل کوله پشتی با الگوریتم های حریصانه و برنامه نویسی پویا مورد توجه قرار گرفت و در نهایت بعد از کشف الگوریتم های فراابتکاری ، حل کوله پشتی با الگوریتم های مختلف فراابتکاری و تکاملی بسیار مورد توجه قرار گرفت.
کاربردهای مسئله کوله پشتی:
مسئلهٔ کوله پشتی میتواند در تصمیمگیریهایی که در دنیای واقعی با آنها روبرو هستیم، مورد استفاده قرار گیرد.
- بریدن کالا بهطوریکه کمترین مقدار به هدر رود.
- انتخاب سرمایهگذاریها و سبد سهام.
- انتخاب داراییها برای مسئلهٔ امنیت داراییهای قبلی.
- ساختن کلیدها برای سیستم رمزنگاری کوله پشتیِ مرکل-هلمن.
یکی از کاربردهای اولیهٔ مسئلهٔ کوله پشتی، طراحی و بارم بندی آزمون است به نحوی که آزموندهنده در پاسخگویی به سؤالات حق انتخاب داشته باشد.
چنانچه بارم بندی سؤالات همگن باشد، مسئله بسیار ساده خواهد شد. برای نمونه، اگر آزمون دارای ۱۲ سؤال، هر سؤال به ارزش ۱۰ نمره باشد، آزمون دهنده باید فقط ۱۰ سؤال را پاسخ دهد تا به بیشینه نمره ممکنِ ۱۰۰ برسد.
اما برای آزمونهایی با بارم بندی نایکسان، مسئله کمی سختتر میشود.
Feuerman و Weiss سیستمی ارائه دادند که در آن دانش آموزان با آزمونی با بارم بندی ناهمگن، با جمع بارم ۱۲۵ روبرو هستند.
از دانش آموزان خواسته میشود با توجه به تواناییهای خود به سؤالات پاسخ دهند.
در اینجا با مسئلهٔ کوله پشتی روبرو هستیم. چه زیر مجموعههایی، جمع نمرهای برابر با ۱۰۰ خواهند داشت؟
برای هر دانش آموز، پاسخگویی به کدام زیر مجموعه از سؤالات، نمرهٔ بیشتری را به ارمغان میآورد؟
انواع مختلف مسئله کوله پشتی
کوله پشتی 0 و 1 :
در این مدل یک شی را یا انتخاب میکنیم (1) یا انتخاب نمیکنیم (0). و هر شی را در صورت انتخاب تنها یک بار میتوانیم انتخاب کنیم. یعنی از هر شی فقط یک دانه را میتوانیم در کیسه قرار دهیم.
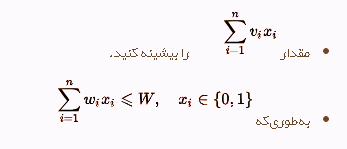
کوله پشتی کسری :
در این مدل، میتوان بخشی از یک شی را برداشت.
مثل حالت قبل ۰ و ۱ی نمیباشد. برای این مسئله راه حال حریصانه وجود داره و به این شکل هست که دزد تا میتواند جنس پرارزش تر را برداشته و درصورتی که نتوانست بیشترین کسر ممکن آن را برمیدارد.
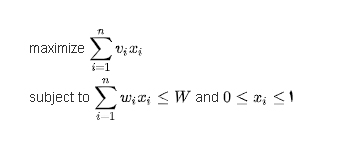
کوله پشتی کران دار :
در کوله پشتی کران دار ، تعداد دفعات انتخاب اشیا عددی صحیح و بزرگتر مساوی 0 است که حداکثر میتواند مساوی c باشد.
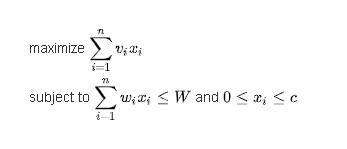
مسئلهٔ کوله پشتی بیکران (UKP):
در این مدل ، هیچ محدودیتی روی تعداد اشیا اعمال نمیشود. یعنی از هر شی، به هر تعداد ممکن میتوان انتخاب نمود.
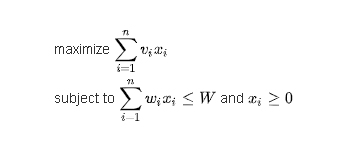
روشهای حل مسئله کوله پشتی
مسئله کوله پشتی را میتوان با بکار گیری روش های زیر حل نمود:
- استفاده از برنامه نویسی پویا ،
- استفاده از الگوریتم حریصانه ،
- استفاده از الگوریتم های فراابتکاری و تکاملی.
ما در متلب24 ، مسئله کوله پشتی 0 و 1 را با الگوریتم های مختلف حل کرده و در دسترس شما عزیزان قرار داده ایم.
فهرست منابع :
ویکیپدیا، ویکی و متلب24 و codesdop.com