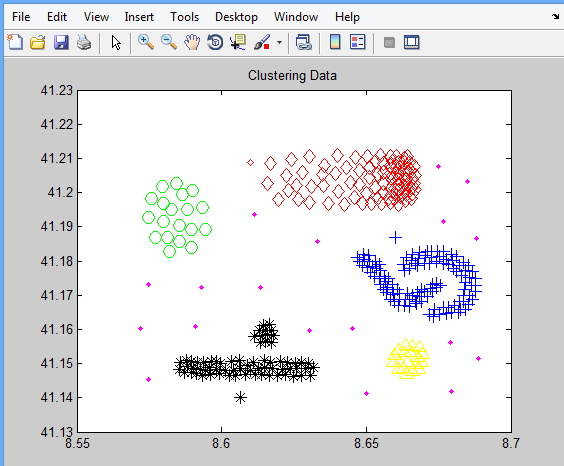
الگوریتم DBSCAN یک روش خوشه بندی است که توسط مارتین استر، هانی-پتر کریگل، یورگ ساندر و شیائووی شو در سال ۱۹۹۶ میلادی (۱۳۷۵ شمسی) ارائه گردیده است. مزیت این روش به نسبت روشهای دیگری خوشه بندی مانند K-Means این است که نسبت به شکل دادهها حساس نمیباشد و میتواند اشکال غیر منظم را نیز در دادهها تشخیص دهد. شکل زیر نمونهای از دادههای دارای شکل کروی است که با روشهایی مانند K-Means در خوشه بندی آن دقت پایینتری به نسبت روش DBSCAN دارند.
دانلود کد الگوریتم dbscan
این الگوریتم نیز به مانند دیگر روشهای خوشه بندی نیازمند روشی برای یافتن نزدیکی دادهها است. میتوان از فاصله اقلیدسی جهت اندازهگیری فاصله (شباهت) استفاده نمود. برای تشریح الگوریتم، نیازمند آشنایی با پارمترهای ε و μ میباشد که توضیح داده میشود:
- هر نقطه از داده با نقاط دیگر فاصلهای دارد. هر نقطهای که فاصله اش با یک نقطه مفروض کمتر از (ε (EPS باشد به عنوان همسانه آن نقطه حساب میشود.
- هر نقطه مفروض که (μ (MinPoints همسایه داشته باشد، یک نقطه مرکزی است.
ارتباط نقاط
همچنین ارتباط نقاط بر اساس وضعیتشان (مرکزی بودن یا نبودن) در هر خوشه، به سه دسته تقسیم میشوند:
- نقاط متصل: نقطه به یک خوشه متصل است که اولاً نقطه مرکزی باشد. ثانیاً با یکی از نقاط داخل خوشه همسایه باشند.
- نقاط دسترسی پذیر: نقطه به خوشه دسترسی پذیر است که نقطه مرکزی نباشد ولی با یکی از نقاط داخل خوشه همسایه باشد.
- اگر نقطه هیچیک از وضعیتهای بالا را نداشته باشد، نویز برای آن خوشه محسوب میشود. همچنین اگر نقطه نسبت به تمام خوشهها نویز باشد، در خوشه نویز قرار میگیرد.
در شکل زیر نقاط قرمز رنگ نقاط مرکزی هستند. نقاط زرد به خوشه مشخص شده دسترسی دارند. نقطه آبی، نویز است. برای شکل زیر μ برابر با ۳ در نظر گرفته شده است.

روند الگوریتم در شبه کد زیر آورده شده است.در ابتدا نقطه به صورت اختیاری انتخاب می شود که قبلا بازدید نشده است. همسایگی این نقطه به شعاع ε بررسی می شود و در صورتی که حداقل تعداد نقاط همسایگی لازم را داشت. خوشه ایجاد می شود وگرنه نقطه نویزی برچسب می خورد.نکته قابل این است که در ادامه ممکن است این نقطه در همسایگی دیگر نقاط قرار گیردو قسمتی از خوشه دیگر شود.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
DBSCAN(D, eps, MinPts) { C = ۰ for each point P in dataset D { if P is visited continue next point mark P as visited NeighborPts = regionQuery(P, eps) if sizeof(NeighborPts) <MinPts mark P as NOISE else { C = next cluster expandCluster(P, NeighborPts, C, eps, MinPts) } } } |
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
expandCluster(P, NeighborPts, C, eps, MinPts) { add P to cluster C for each point P' in NeighborPts { if P' is not visited { mark P' as visited NeighborPts' = regionQuery(P', eps) if sizeof(NeighborPts')>= MinPts NeighborPts = NeighborPts joined with NeighborPts' } if P' is not yet member of any cluster add P' to cluster C } } regionQuery(P, eps) return all points within P's eps-neighborhood (including P) |
مزایا و معایب
مزایا:
- سریع برای دادههای با بعد کم
- یافتن خوشهها برای اشکال نا منظم و کروی
- تشخیص نقاط نویز
معایب:
- نقاط مرزی که میتوانند در دو خوشه نیز باشند، ممکن است به هریک از خوشهها تعلق گیرند.
- این روش بنابه تغییرات در μ و ε رفتار غیرقابل پیش بینی میتواند داشته باشد
جهت دریافت کد متلب الگوریتم dbscan به روی لینک زیر کلیک کنید: