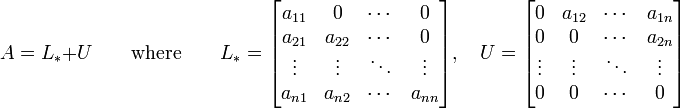Gauss-Seidel
حل دستگاه معادلات خطی به روش گاوس سایدل
روش گوس سایدل یک روش تکراری در حل دستگاه معادلات خطی است که در جبر خطی مورد بحث قرار می گیرد. نام این روش از روی ریاضیدانان آلمانی کارل فریدریش گاوس و فیلیپ لودویگ ون سایدل نهاده شدهاست. اگرچه از این روش میتوان در هر ماتریسی که دارای درایه قطری صفر نباشد استفاده کرد، اما فقط در صورتی همگرایی تضمین میشود که ماتریس مثبت معین و یا غالب قطری باشد.
این برنامه به زبان متلب نوشته شده است که n (تعداد معادلات خطي در n معادله n مجهول) را گرفته و سپس ضرايب مجهولات و سپس مقادير معلوم را دريافت کرده و با استفاده از روش گوس سایدل (Gauss-Seidel) معادله را حل و مقادير مجهولات را بدست آورده و چاپ میکند.
جهت خرید کد متلب روش گوس سایدل از بخش زیر اقدام کنید و بصورت آنلاین خرید و دانلود کنید
[parspalpaiddownloads id=”69″]
ایمیل: matlab24ir@gmail.com و یا info@matlab24.ir
————————————————————————————–
برای یک سیستم مربعی با n معادله ی خطی و دارای مجهول x داریم:
که در آن:
اگر A را به ماتریس پایین مثلثی و بالا مثلثی L* و U تجزیه کنیم:
معادلات خطی سیستم به شکل زیر بازنویسی خواهند شد:
روش گاوس سایدل از روش تکراری برای حل قسمت چپ عبارت جهت به دست آوردن x بهره میبرد، و بدین منظور از مقدار قبلی x در سمت راست عبارت استفاده میکند. میتوان آن را به صورت زیر نوشت:
و با استفاده از خواص ماتریس مثلثی L* میتوان x(k+1) را به صورت زیر به دست آورد:
در واقع برای محاسبه xi(k+1) به همه عناصر x(k) به جز خود xi(k) نیاز خواهد شد.
محاسبات تا زمانی ادامه داده میشود تا در تکراری خاص به خطایی کمتر از مقدار مورد نظر برسیم.