حل کوله پشتی با الگوریتم tabu search
در این کار ما مسئله کوله پشتی صفرو یک را با الگوریتم جستجوی ممنوعه حل کرده ایم
برای دریافت کد حل مسئله کوله پشتی با الگوریتم توده ذرات یا Tabu Search از بخش زیر اقدام کنید
کد متلب حل کوله پشتی ۰ و ۱ با الگوریتم جستجوی ممنوعه (Tabu Search) به همراه فایل توضیحات خط به خط و روش حل
کد به همراه فایل توضیحات خط به خط کد
جهت خرید از بخش زیر اقدا کنید و بصورت انلاین فایل را خریداری و دانلود کنید
[parspalpaiddownloads id=”58″]
ایمیل : matlab24ir@gmail.com و یا info@matlab24.ir
شماره تماس : ۰۹۱۳۹۹۳۵۳۶۰
————————————————————————————–
توضیحات مسئله کوله پشتی :
مسئله کوله پشتی که با عنوان های Knapsack یا Rucksack مطرح می شود، مسئله ای در بهینه سازی ترکیبیاتی است. فرض کنید مجموعه ای از اشیا، که هر کدام داری وزن و ارزش خاصی هستند در اختیار دارید. به هر شی تعدادی را تخصیص دهید به طوری که وزن اشیا انتخاب شده کوچکتر یا مساوی حدی از پیش تعیین شده، و ارزش آنها بیشینه شود. علت نامگذاری این مسئله، جهانگردی است که کوله پشتی ای با اندازه ی محدود دارد و باید آن را با مفیدترین صورت ممکن از اشیا پر کند.
فرض کنید 
جسم داریم که از 
تا شماره گذاری شده‌اند. جسم 
ام ارزشی معادل 
و وزنی برابر با 
دارد. معمولاً فرض می شود که وزن ها و ارزش ها نامنفی اند. برای ساده تر شدن نمایش، بدون کم شدن از کلیت مسئله می توان فرض کرد اشیا به ترتیب صعودی بر حسب وزنشان مرتب شده‌اند. بیشترین وزنی که می توان در کوله پشتی حمل کرد،
است.
معروف ترین نوع از این مسئله، مسئله ی کوله پشتی ۰ و ۱ است. یعنی تعداد از هر شی، یا ۰ است (آن شی را انتخاب نمی‌کنیم) یا ۱ ( آن شی انتخاب می شود). مسئله ی کوله پشتی ۰ و ۱ را می توان به این صورت، به زبان ریاضی بیان کرد:
- مقدار
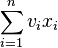را بیشینه کنید. - به طوری که
