کد موازی الگوریتم دایکسترا Paralell DIJKSTRA
در نظریه گراف، الگوریتم دایکسترا یکی از الگوریتمهای پیمایش گراف است که توسط دانشمند هلندی ، اِدْسْخِر دایْکْسْترا در سال ۱۹۵۹ ارایه شد.
این الگوریتم یکی از الگوریتمهای پیمایش گراف است که مسئلهٔ کوتاهترین مسیر از مبدأ واحد را برای گرافهای وزنداری که یال با وزن منفی ندارند، حل میکند و در نهایت با ایجاد درخت کوتاهترین مسیر، کوتاهترین مسیر از مبدأ به همهٔ رأسهای گراف را به دست میدهد. همچنین میتوان از این الگوریتم برای پیدا کردن کوتاهترین مسیر از مبدأ تا رأس مقصد به این ترتیب بهره جست که در حین اجرای الگوریتم به محض پیداشدن کوتاهترین مسیر از مبدأ به مقصد، الگوریتم را متوقف کرد.
الگوریتم دایکسترا یکی از الگوریتمهای مورد استفاده برای محاسبه کوتاه ترین مسیر تک منبع (single-source shortest path) است و مشابه الگوریتم پریم میباشد در صورتی که گراف یال با وزن منفی داشته باشد، این الگوریتم درست کار نمیکند و میبایست از الگوریتمهای دیگر نظیر الگوریتم بلمن-فورد که پیچیدگی زمانی آنها بیشتر است استفاده کنیم.
خط مشی الگوریتم دایکسترا، مشابه با روش حریصانهٔ استفاده شده در الگوریتم پریم برای پیدا کردن زیر درخت فراگیر بهینه است.
روند الگوریتم دایکسترا مطابق زیر میباشد:
۱- انتخاب راس مبدا
۲- مجموعهٔ S، شامل رئوس گراف، معین میشود. در شروع، این مجموعه تهی بوده و با پیشرفت الگوریتم، این مجموعه رئوسی که کوتاه ترین مسیر به آنها یافت شده است را در بر میگیرد.
۳- راس مبدا با اندیس صفر را در داخل S قرار میدهد.
۴- برای رئوس خارج از S، اندیسی معادل، طول یال + اندیس راس قبلی، در نظر میگیرد. اگر راس خارج از مجموعه دارای اندیس باشد، اندیس جدید کمترین مقدار از بین اندیس قبلی و طول یال + اندیس راس قبل، میباشد.
۵- از رئوس خارج مجموعه، راسی با کمترین اندیس انتخاب شده و به مجموعهٔ S اضافه میگردد.
۶- این کار را دوباره از مرحلهٔ ۴ ادامه داده تا راس مقصد وارد مجموعهٔ S شود.
در پایان اگر راس مقصد دارای اندیس باشد، اندیس آن نشان دهندهٔ مسافت بین مبدا و مقصد میباشد. در غیر این صورت هیچ مسیری بین مبدا و مقصد موجود نمیباشد.
همچنین برای پیدا کردن مسیر میتوان اندیس دیگری برای هر راس در نظر گرفت که نشان دهندهٔ راس قبلی در مسیر طی شده باشد. بدین ترتیب پس از پایان اجرای الگوریتم، با دنبال کردن رئوس قبلی از مقصد به مبدا، کوتاه ترین مسیر بین دو نقطه نیز یافت میشود.
ما در این کد الگوریتم دایکسترا را بصورت موازی در متلب آماده کرده ایم . این کد با استفاده از SPMD موازی سازی شده است. این کد کوتاهترین مسیر از راس مبدا تا همه رئوس دیگر را پیدا میکند.
این کد با استفاده از SPMD در متلب موازی سازی شده است.
روال موازی سازی به این صورت می باشد که با استفاده از ابزار matlabpool موازی سازی انجام میشود و برای انجام کار ابتدا راس های گراف بین worker ها تقسیم میشوند و سپس در یک حلقه تکرار مراحل کار انجام میشود در هر مرحله از تکرار حلقه، هر worker نزدیک ترین راس از بین راس های خود به راس مبدا (راس های متصل شده) را انتخاب میکند و سپس اطلاعات همه workerها به client فرستاده میشود و از بین رئوس انتخاب شده توسط workerها ، راسی که کمترین مسیر را داشته است انتخاب میشود و این روال تا افزوده شده همه راس ها به مجموعه جواب ادامه می یابد
جهت دریافت کد از بخش زیر اقدام کرده و بصورت آنلاین محصول را خریداری و دانلود کنید
| [parspalpaiddownloads id=”108″] |
ایمیل :matlab24ir@gmail.com و یا info@matlab24.ir
شماره تماس: 09120563264
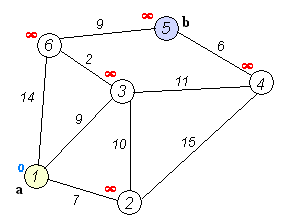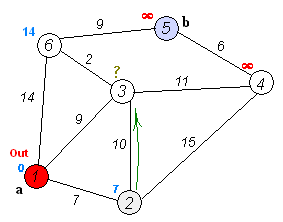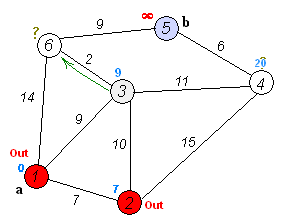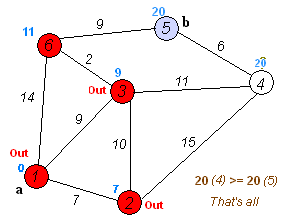
گراف در نظر گرفته شده شامل 6 گره و 8 یال می باشد که بصورت زیر یالها وصل شده است:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
N0--15--N2-100--N3 \ | / \ | / 40 20 10 \ | / \ | / N1 / \ / \ 6 25 / \ / \ N5----8-----N4 و در نهایت کوتاهترین مسیر از گره 0 به همه گره های دیگر که بصورت زیر می باشد را نمایش میدهد: |
|
1 2 |
From 0 to: 0 1 2 3 4 5 Distance: 0 35 15 45 49 41 |
جهت دریافت کد از بخش زیر اقدام کرده و بصورت آنلاین محصول را خریداری و دانلود کنید
[parspalpaiddownloads id=”108″]



لطفا هزینه دریافت کد موازی الگوریتم دایجسترا را بفرمایید.
سلام
هزینه کار و لینک خرید به مطلب اضافه گردید
با تشکر از شما
سلام. ببخشید من هر چی می گردم نمی تونم لینک دانلود و پرداخت هزینه رو برای این برنامه پیدا کنم.
سلام. دکمه خرید را کلیک کنید
البته موقتا به دلیل اختلال در درگاههای پرداخت امکان خرید آنلاین دچار اختلال شده است.
میتوانید مبلغ را کارت به کارت کرده و کد را برای شما ایمیل خواهیم کرد.
با تشکر